题目
给你一个下标从 0 开始的整数数组 nums 和一个 非负 整数 k 。
在一步操作中,你可以执行下述指令:
- 在范围
[0, nums.length - 1]中选择一个 此前没有选过 的下标i。 - 将
nums[i]替换为范围[nums[i] - k, nums[i] + k]内的任一整数。
数组的 美丽值 定义为数组中由相等元素组成的最长子序列的长度。
对数组 nums 执行上述操作任意次后,返回数组可能取得的 最大 美丽值。
注意:你 只 能对每个下标执行 一次 此操作。
数组的 子序列 定义是:经由原数组删除一些元素(也可能不删除)得到的一个新数组,且在此过程中剩余元素的顺序不发生改变。
示例 1:
1 | 输入:nums = [4,6,1,2], k = 2 |
示例 2:
1 | 输入:nums = [1,1,1,1], k = 10 |
提示:
1 <= nums.length <= 1050 <= nums[i], k <= 105
题解
1 | class Solution { |
知识点
排序 + 滑动窗口
根据子序列和美丽值的定义可知:最终所求结果和元素顺序无关。因此,可以将原数组排序,得到如下图的区间图:
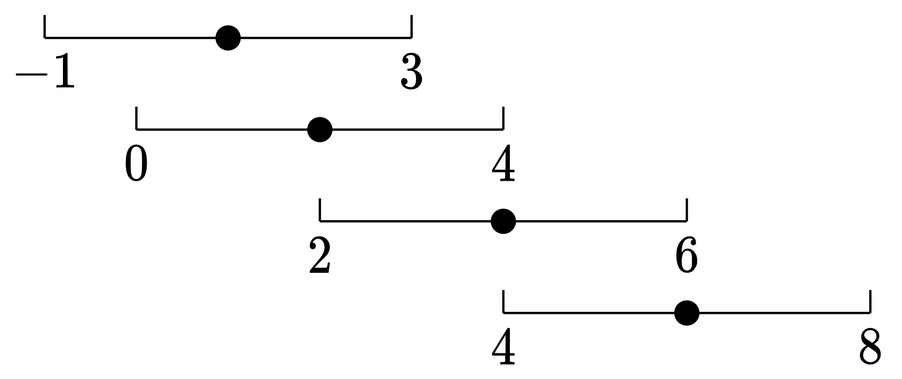
题目所求的相等元素组成的最长子序列,相当于选出若干闭区间,交集不为空。
经过排序后,区间是连续的,只需考虑最左边区间[left−k,left+k]和最右边区间[right−k,right+k]的交集不为空,即可保证之间的这些区间也不为空,即:left+k >= right-k。